I just got home from a five-week tour in Europe and finally have some time to do what I call research. The way I see it, being a touring musician is a bit like being a scientist: you spend a bunch of time in the lab, and you find something that you’re excited about; then you have to go out and give a bunch of seminars to tell the world about it. But very soon you’re itching to get back to the lab, because you want to discover the next thing. So here I am, at home and doing research, which for me, right now, in between practicing piano and writing tunes, means getting into a computer music programming environment called SuperCollider.
Yesterday I was fooling around with it and suddenly realized that with SuperCollider, I could do something I’d been wanting to do for years, which is to make a recording of rhythm becoming pitch, and back again. You see, rhythm and pitch are exactly the same thing, only at very different speeds. How’s that, you ask? Well, let’s start with the harmonic series:
The harmonic series is what you get when you take a string, on a guitar, say, and start dividing it up. So let’s say you tune your string to a low C, the lowest note on the staff above. Then you divide it in two, so only half of the string is ringing. That note, as Pythagoras discovered a long time ago, sounds exactly an octave higher than the fundamental. Now you divide it in thirds, and you realize that that note is exactly an octave and a perfect fifth above the fundamental, a G. Now here’s the interesting part: the octave vibrates at exactly twice the frequency of the fundamental, and the octave + fifth vibrates at 3 times the frequency of the fundamental. In other words, divide a string in 2 and it vibrates twice as fast; in 3 and it vibrates 3 times as fast. And so on through the harmonic series — I’ve written down the first 8 notes of it above. The major third (E 2 octaves above the fundamental), for example, shows up when you divide the string in 5 and it vibrates 5 times as fast as the fundamental.
How does this relate to rhythm? Let’s think about the interval of an octave. If we play a low C and the C an octave above that at the same time, we’ll have one note vibrating at one frequency and the other vibrating 2 times as fast. If you looked at the sound waves next to each other, they would look like this:
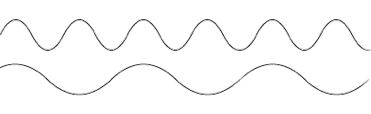 Now consider just the crests of each wave, the moment where they reach their maximum. In the time between two crests of the bottom wave (the fundamental), the top one (the octave) crests twice. If we were to write this out in rhythmic notation, it would look like this:
Now consider just the crests of each wave, the moment where they reach their maximum. In the time between two crests of the bottom wave (the fundamental), the top one (the octave) crests twice. If we were to write this out in rhythmic notation, it would look like this:
That’s a very simple rhythm: 2 for 1. Any child can tap it on her knees. But did you know that if you sped a recording of her tapping this rhythm on her knees up about a hundred times, you would actually hear two pitches an octave apart? Don’t take my word for it, check it out:
;
Pretty amazing, right? For most of us, this will be the first time we’ll have consciously witnessed rhythm turning into pitch, then turning back to rhythm. At the beginning, you can hear the “fundamental” in the left channel clicking away, and the “octave” in the right channel clicking twice as fast (2 clicks for every one in the left channel). Then, as it speeds up, there’s a period where you can’t really hear rhythm — the clicks start to blur into each other. Then something magical happens — you start to perceive pitch, first as a very low note, then as it speeds up, as a higher and higher note. Then the octave below starts to emerge as well. By the time we reach the highest point, the two notes are clear, the fundamental in the left channel and the octave in the right.
Why does this work? Well, it turns out that we have two systems for perceiving music. For slow things, our consciousness distinguishes individual events and interprets them as what we call “rhythm”, such as the child tapping on her knees. For very fast things (like when the taps get very close together), our consciousness isn’t fast enough to distinguish the individual events, and our pitch hearing kicks in, guided by those tiny hairs in our cochlea, each one specialized in resonating at a certain pitch.
That is, when rhythm is very fast, we hear it as pitch. In the same way that we can say one song is “faster” than another (and we could measure that difference in BPM), we can also say that one pitch is “higher” than another (and we could measure that difference as a musical interval). The thing that some people may not realize is that when we’re making those comparisons, we’re talking about the very same thing: a “high” pitch could also be called a “fast” pitch.
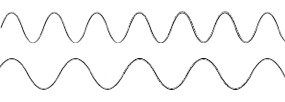
So here’s where it gets interesting. We just heard what an octave sounds like. That’s a very simple rhythm. How about a fifth? If you look back at the harmonic series diagram, you’ll see that if we want to listen to a perfect fifth (the first G from the bottom against the C right below it), we should be listening to two tones that vibrate in a 3 to 2 relationship — that is, the upper one vibrates 3 times in the time it takes the bottom one to vibrate twice:
Looking at the crests of the waves in musical notation gives us:
That’s a slightly more complicated rhythm, but kids can still do it with a little practice. Now hear it become pitch:
;
Again, I find the transition between our two systems of hearing fascinating — it’s as if you could see slow flashes of light speed up and gradually morph into a color (is that feasible? Not as far as I can tell). And it only gets more interesting as the rhythms get more complex. A perfect fourth is a 4 to 3 relationship,
and sounds like this:
;
My favorite is the major third, a 5 to 4 relationship that is an awesome rhythm (I use it all the time in my music) and also happens to be a lovely interval. Would you have guessed that such a consonant interval would have such a thorny rhythm behind it? Next time you tap it out on your knees, try to get your mind around the idea that you’re playing a really slow major third.
;
The minor third is great, too — a 6 to 5 relationship
that sounds like this:
;
* * *
We could go on with these intervals — the major sixth, for example, a 5 to 3 relationship, is particularly nice — but what I really wanted to know as I experimented with this last night was: what does a triad sound like, rhythmically? Well here it is. Let’s look at a major triad first, which as you can easily figure out from the harmonic series diagram, is a 6 to 5 to 4 relationship:
This isn’t a rhythm that you’re going to hear a kid tapping out, but a good drummer could work it up relatively quickly. The difficulty is in the way it mixes ternary (triplet) and binary divisions of the beat. Still, it’s pretty catchy. Here I’ve put the lowest note in the middle, the third in the left speaker, and the fifth in the right:
;
Pretty crazy, right? How an honest-to-goodness major triad could emerge out of that clicky mess? Now we’re left with the minor triad. Interestingly, even though we often think of a minor triad as a more complex sound than a major one (or at least, sadder) it’s a simpler rhythm in that it’s entirely made up of ternary divisions of the beat. But it also takes longer to resolve. So you could say it’s more in phase with itself, but also more ponderous; less cognitive dissonance, perhaps, but more internal debate.
It sounds like so:
;
If you’re wondering how I got those ratios (15 to 12 to 10), it’s like this: take the minor third from the harmonic series, between the E and G in the first diagram above. That’s a 6 to 5 relationship. Now we need the fifth, which we can get by multiplying the root note (the E) by 3/2, giving us 7.5. Now multiply all 3 numbers by 2 so that we can be dealing with whole numbers, and voilà: 15/12/10.
* * *
One last thing. The waves I’ve drawn for you here are sine waves, but if you know anything about sine waves, you’ll quickly realize that the sounds you’re hearing on these recordings, even when things are going very fast and you’re hearing clear pitches, aren’t sine waves. The clicks that you hear at the beginning and end of the tracks are what are called impulses, basically the quickest move the speaker can make. The wave for an impulse looks like this:
These sound like clicks when you hear them individually. But when they get very close together,
we stop hearing the clicking and instead, we hear the same pitch that we would hear if each impulse were the crest of a sine wave. Our ear can clearly tell the difference, though, by the timbre of the sound: the pitches made of impulses are aggressive and tinny to the ear, whereas ones made of sine waves are pleasant and full:
The difference in timbre is huge. Our sense of pitch, however, is activated just the same.
* * *
One very last bonus track: remember the major sixth I talked about earlier, the 5 to 3 relationship? That’s such a nice rhythm (my friend Gabriel Kahane, for one, uses it throughout his song Durrants) that I’ll give it to you here
in all its transformative glory:

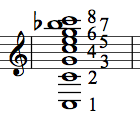





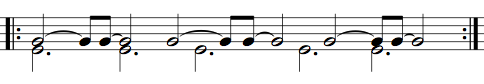





Pingback: Scratch My Brain » Dan Tepfer // Rhythm / Pitch Duality: hear rhythm become pitch before your ears
Reminds me of Henry Cowell’s “New Musical Resources.” Nice!
Thanks Marc — I wasn’t aware of Cowell’s work on this topic & am ordering New Musical Resources now!
If my gray brain cells serve me right, our mutual friend Keith Kirchoff discovered some of Cowell’s music while he was doing some research at the NYC Library and later performed some of his music. Indeed, we exist in a small world.
Wally
Oh yes, that book by Cowell is a gem! Found a copy for free that the public library in my town was getting rid of due to lack of space, didn’t read it for three-or-so years, but when I finally did, it opened up my ears. Also read his comments on music and noise in Audio Culture.
Pingback: Rhythm as Pitch | Jeff Albert's Research
Dan,
I love the auralization of the concept. Very cool. It made me want to play with different ratios, so I wrote something in ChucK that works similarly. I’d be curious to see your SuperCollider code as well, if you are up to share. My ChucK version is at http://research.jeffalbert.com/2012/rhythm-as-pitch/
Peace,
Jeff
Hey Jeff,
Glad you enjoyed the post. The auralization is definitely the interesting part, I agree. My code is incredibly simple; just a couple lines using MouseX as frequency, and adjusting for the specific cases. See below.
Be well,
–d
// 1/2
{ Impulse.ar([1*MouseX.kr(0, 500), 2*MouseX.kr(0, 500)], 0.0, 0.2) }.play;
// 2/3
{ Impulse.ar([2*MouseX.kr(0, 100), 3*MouseX.kr(0, 100)], 0.0, 0.2) }.play;
// 3/4
{ Impulse.ar([3*MouseX.kr(0, 100), 4*MouseX.kr(0, 100)], 0.0, 0.2) }.play;
// 4/5
{ Impulse.ar([4*MouseX.kr(0, 100), 5*MouseX.kr(0, 100)], 0.0, 0.2) }.play;
// 5/6
{ Impulse.ar([5*MouseX.kr(0, 100), 6*MouseX.kr(0, 100)], 0.0, 0.2) }.play;
// 3/5
{ Impulse.ar([3*MouseX.kr(0, 100), 5*MouseX.kr(0, 100)], 0.0, 0.2) }.play;
//major triad
(
{ Impulse.ar([5*MouseX.kr(0, 100), 6*MouseX.kr(0, 100)], 0.0, 0.2) }.play;
{ Impulse.ar([4*MouseX.kr(0, 100), 4*MouseX.kr(0, 100)], 0.0, 0.2) }.play;
)
//minor triad
(
{ Impulse.ar([12*MouseX.kr(0, 25), 15*MouseX.kr(0, 25)], 0.0, 0.2) }.play;
{ Impulse.ar([10*MouseX.kr(0, 25), 10*MouseX.kr(0, 25)], 0.0, 0.2) }.play;
)
Hi, great post, fascinating stuff! I am a newbie with SuperCollider, and your examples sound static, they don’t sound the way they sound in the post (without the increasing speedy tempo). How to get this increasing effect? Thanks!
Hi Gahariet,
Try moving your mouse around on the screen! That should do it.
Dan
Haha, silly me! Thanks!
Nice post! really interesting, i’ve found the pdf of “new musical resources” in case you’re interested in checking it out
http://www.google.pt/url?sa=t&rct=j&q=&esrc=s&source=books&cd=1&ved=0CDYQFjAA&url=http%3A%2F%2Fzztt.org%2Flmc2_files%2FCowell_New_Musical_Resources.pdf&ei=hjTRUMTFFMTRhAeUl4GYAw&usg=AFQjCNHLPNjeaDQTNYGTdM9N-h2Na7hDvw&sig2=gjnsHbjRpuNDk5FP_36OCg&bvm=bv.1355534169,d.ZG4&cad=rja
and thanks for de major triad example!!!!
now i know how to score a motorcycle accell for orchestra =)
Cheers from Portugal!
hey daniel,
many thanks for the link! i have a copy of ‘new musical resources’ coming in the mail, but it’s nice to have a copy to carry around electronically.
let me know if you use any of this in a piece…
cheers from brooklyn,
dan
Ps- you should get this to AriHoenig he would probabli play the acell examples on the drums =)
Oh yeah, this would be a cinch for Ari!
Great job. Stockhausen did something similar in the 50’s. If you mess around with a Buchla synth you can do the same kind of thing. I love how you explained everything clearly and simply and I really love your examples. Again great job!!!
Thanks Ken— glad you enjoyed it. I’m learning a lot from these comments — wasn’t even familiar with Buchla until now. I take it you’re referring to Kontakte, re. Stockhausen?
fascinating!
Jim Tenney’s piece “Spectral Canon for Nancarrow,” which Nancarrow punched out on a piano roll, works out this process using just intonation. Jim’s piece stopped halfway through the process, but Clarence Barlow completed it (it was an arc form, and he completed it) with a computer realization.
Hi Mary Jane,
Just got around to listening to Tenney’s piece. Found it here:
http://www.youtube.com/watch?v=hUrfKBnQ9a4
You’re right — it’s a perfect demonstration of the rhythmic aspect of what I’m talking about in this post. And if it could be sped up another 50 times or so, you would probably start to hear pitch from the rhythms, too, although the fact that each “impulse” (the notes on the piano) is already pitched would complicate things. Thanks for telling me about this!
Very cool, Dan! Just shared it on our Facebook page https://www.facebook.com/jazzheaven
Something else that jumped out at me while listening to these–when you hear a certain interval coming from an engine (of a propeller, for example), you’re really just hearing the speeded-up version of a certain ratio. Great stuff!
Right, exactly! But usually you’re only hearing one pitch, unless two motors are going at the same time, and even then, the interval between them will almost always be changing, whereas in these examples, the relationships stay fixed.
Best visual analog is cinema. What you’re describing is “persistence of hearing”, i.e. like persistence of vision, or, when film frames speed up fast enough so that we perceive motion….or to put it another way, we no longer perceive the gaps.
Another visual analogy is pointillism, where small dots of color combine to give the appearance of new colors and shapes. This is how comics work: by combining only four matrices of inks (cyan, yellow, magenta, and black) to make any color you can imagine.
Humans and other animals with eyes have a flicker fusion frequency – that is the rate the eye can detect the on/off cycle of a light. If you turn the light off and on quickly enough, the brain doesn’t perceive any change. Flourescent tube lights flicker on and off rapidly, the only time we notice this is when the bulb is dying and the cycle slows down to a rate below our flicker fusion frequency
Dan, you might want to check out Stockhausen’s ‘Kontakte,’ a great piece which explores this in really interesting ways.
http://en.wikipedia.org/wiki/Kontakte_(Stockhausen)
Thanks Sam — just bought Kontakte and listening to it as I write.
From the Wikipedia article:
The most famous moment, at the very center of the work, is a potent illustration of these connections: a high, bright, slowly wavering pitch descends in several waves, becoming louder as it gradually acquires a snarling timbre, and finally passes below the point where it can be heard any longer as a pitch. As it crosses this threshold, it becomes evident that the sound consists of a succession of pulses, which continue to slow until they become a steady beat. With increasing reverberation, the individual pulses become transformed into tones once again.
So Stockhausen was exploring the transition from pulse perception to frequency perception, but was he also interested in interval ratios as rhythm generators, the way I’ve now learned Cowell was? I find hearing a chord move through the transition pretty amazing, because then we’re talking about polyrhythms and not just pulse.
Just got to the part of Kontakte described in the Wikipedia article. Super effective. Pretty amazing that this is from 1958…
Hi Dan – thanks for the post, nice to have concrete examples to listen to.
“So Stockhausen was exploring the transition from pulse perception to frequency perception, but was he also interested in interval ratios as rhythm generators, the way I’ve now learned Cowell was?”
Kind of – Gruppen, for example, is structured on the idea of “formants”, which is KS’s corruption of harmonic partials having different rhythmic relationships to one another. Which is why you get all the crazily precise tempo indications in that piece – they’re all derived from harmonic series ratios. (I think I’m recalling that correctly. He wrote about all this in one of his Die Reihe articles.)
Someone else you might be interested in is Ben Johnston, who really did pursue this idea for a while, and much more I think from Cowell’s version of it. Knocking Piece, 1962, for example (http://www.youtube.com/watch?v=hv3Kilnw_TU) is a “rhythmified” version of the pitches of an earlier serial piece (A Sea Dirge).
The way Gruppen works is almost like Tim describes: the tempos are not based on the harmonic series, but on 12-division equal temperament. There are 12 tempos between MM=60 and MM=120 (13 tempos if you include these two, of course, but they’re actually a tempo octave apart, so considered equivalent). Then, each long duration in the given tempo is subdivided evenly into crotchets, triplets, quavers, quintuplets, etc.: basically like an overtone series! So you could think of Gruppen as a piece of pitch-based serial music slowed down until the pitches have shifted into the rhythm domain! (And no, you can’t really “hear it that way” – whatever that means – but what a remarkable idea for a piece, esp for 1955!) For further details seek out Stockhausen’s essay “…wie die Zeit vergeht…” which is also available in English as “…how time passes…”
http://en.wikipedia.org/wiki/Gruppen_(Stockhausen)
Just to be more explicit:
rhythm => pitch
rhythm ‘formants’ => timbre
duration => wavelength
meter => timbral ‘period’
Phillipp, I’m grasping rhythm accelerating into pitch, and duration into wavelength.
Are what you call the rhythm ‘formants’ in fact superimpositions of various rhythms (just like overtones producing the harmonic make-up of a specific timbre)?
If so, is the ‘timbral period’ the minimum time-length of a cycle of overtones required to produce a given timbre, thus the meter or time-signature we are familiar with in the rhythmic domain?
Also Ben’s String Quartet #4 (Amazing Grace) makes relationships between interval ratios and rhythmic ratios.
Dan,
i really loved reading and listening to this.
very interesting and clearly stated.
thank you for that!
Thanks very much, Chris! Really means a lot to me that you got something out of this. We’ll have to try these ideas out with instruments one of these days.
Nice post, Dan. I have a similar set of resources at my blog. I just used Audacity software’s click track, setting up a variety of frequency ratios and speeding them up by 400% over and over again.
The more people that know and understand this material, the better. Surprisingly few musicians do — which seems like a painter not understanding color. My classes at NEC are always amazed when I show them these concepts.
Here’s the link:
http://www.warrensenders.com/journal/?p=4820
Hi Dan,
I run an NPO music school in Hout Bay, Cape Town, Kronendal Music Academy, and we are always fascinated by these bits of interesting musical miracles…
So, thanks for this – great to hear the rhythms in real time… Have you come across a book called “The Cosmic Octave” by Hans Cousto? (Swiss Mathematician and Musicologist) Same concepts discussed etc, (plus many more) including the expansion on sound = colour frequencies… so, each tone has the same frequency as a colour does; eg g = orange/red; c# = blue green… and the frequency of the sun around the earth and the earth on its axis, corresponds to this etc etc etc. So, I love to think that while I am playing I am also playing in colours! (not to mention the magnificent rhythms you have shown us here too!) Can feel like it’s getting a little “esoteric”, but it’s all just maths and science in the end. And wonderful sound 🙂
Check out the table: http://www.planetware.de/octave/table.html
best
Ms Dwyn G
Pingback: From the bench : pitch == rhythm
Psychoacoustic studies in pitch perception are endlessly interesting and yield beautiful and musical results like these. Its interesting that the perception of variable pulse trains (as in your examples above) and perception of variable sine tones are quite different, i.e. if the frequency of a sine tone is below 20 Hz it would not be audible to human ears. That is we can only use pulse trains (antialised sawtooth, impulses, etc.) to demonstrate this phenomenon.
There have been many interesting experiments that document the variety of human pitch perception…especially temporal pitch perception, which led to the design of cochlear implants among other things.
Tenney was really interested in all these ideas when he was at Bell Labs in the 60s and I think one of the most elegant was his fascination of the Shepard Tone and slow rhythmic periodicity…as heard in “For Ann (rising)”…different from the discussions above, but just as fun (!)
http://www.youtube.com/watch?v=RqRd555v0Hg
This is wonderful, Dan. So simple and plainly true, and yet such a surprise. Fantastic to witness an abstraction made concrete. Yay!
Just realized then that perfect pitch and perfect time are the same thing. That’s another mind-blower.
Nice! Hadn’t thought about that, but you’re right: the ability to keep a steady beat is the same as being able to keep a steady pitch, only on different time scales…
Much appreciation and gratitude for your creative exploration and exciting contributions. I was reminded of the ‘whoosh whoosh whoosh’ of the raven which crossed my path while hiking this morning, and then the buzzing of the fly that circled my head in my sit spot a few moments later. One was ‘rhythm’ and the other ‘tone.’ Both were periodicity, with wildly different frequencies.
Music is the pure magic that we are.
I was curious to hear the flat 9 move from rhythm to tone, because dissonance aligns so infrequently. I am also mystified how ‘dissonance’ can sound so lovely in context (the opening tritone of ‘Blue in Green,’ for instance).
Thanks for your bold and daring thoughts.
A book you will love is Joscelyn Godwin’s book, “The Mystery of the Seven Vowels.” Godwin is a virtuoso harpsichordist and also a music teacher (at Colgate University). (He is also the member of some secret mystic cult). The book describes how vowels are tonal, and yet the difference between, say, ‘e’ and ‘a’, if both articulate on the same fundamental, concerns the intensity of the overtones. This is of course what distinguishes the middle C on a piano versus a flute. We can somehow decipher overtone intensities and distinguish vowels from one another when speaking. This points to the profoundly sophisticated musical context from which human language evolved and within which it finds continued expression.
http://www.amazon.com/The-Mystery-Seven-Vowels-Practice/dp/0933999860
Great book, brilliant man. I had the tremendous honor of studying under Joscelyn at Colgate in the late 1980s.
I think these sorts of illusions are really cool.
However, the situation is even stranger than you describe.
One thing has to do with pitch. You describe pitch as being how fast the sine wave moves up and down. True, sine waves do indeed have pitches. But what you are describing is actually frequency, which is not the same thing. In addition to the commonly-known pitches of pure tones and harmonics, there are also a lot of really weird ways to make pitches where there is no sound at all at the frequency you hear the pitch at.
So then what is pitch? The truth is nobody is quite sure. Let me rephrase that: lots of people are sure, but nobody has been able to convince everyone else that they are right.
Another weird thing is with octaves. The reason octaves are significant is because two pitches that are otherwise the identical but separated by one octave are very hard to tell apart, even though the frequency of one is twice the other, and we are normally sensitive to much smaller frequency changes. Nobody is entirely sure why that is, either, but it doesn’t appear to be part of the mechanics of the ear. Also, if you combine two sounds that are off by one octave, you only hear one pitch (which you can hear in your illusions),
There are also weird things that happen with rythms. When do we hear two sounds as a rhythm, and when do we hear them as two independent sets of sounds? There are a lot of rules regarding this, including where the sounds are coming from, whether they start at the same time, whether things like loudness and frequency changes sync up, and so on. It is possible to manipulate this on the fly by playing with these parameters, but two periodic sounds that start off seeming like separate sources will tend to fuse into one rhythm the longer you listen to them, only to be suddenly broken up again when one sound does something the other doesn’t. You may even notice this when listening to the examples here (I did at least).
Another interesting thing has to do with how our ears and brains handle sequential sounds. If two sounds are too close together, you won’t hear the second. There are even cases where a later sound will make you unable to hear a sound that came before it!
Really well written, clear and fascinating. Good work. Thanks!
Hey Dan,
Have you heard the music of Ben Johnston? I’m assuming you have, but if you haven’t, he takes this “rhythm from pitch” concept to an extreme. Rhythms are derived from their pitch ratios. Basically, if he’s writing fifths, there will be a 3:2 rhythmic relationship, a just intone major third will have a 5:4 relationship, and so on all the way up the overtone series.
If you haven’t heard his music you should start with his 4th string quartet, or the amazing grace quartet as it’s often called. Really one of the masterpieces of the 20th century! Here’s a link to a pretty good performance, really hard stuff to play. http://vimeo.com/17298063
Pretty rad stuff!
Ben
I’ve been using Absynth to do this for my students in Acoustics for years. Always blows their minds! In Absynth, you can just draw a very short duty-cycle pulse wave form, which works both a the rhythm and the intervals. Then if you have pure intervals tuned in a programmed “temperament” (which ain’t no temperament ’cause there’s nothing tempered), you just transpose the whole thing down 73 notes and play the interval on the keyboard, which sounds like a rhythm, then transpose it back up slowly until it sounds like an interval.
Nice. It’s so simple, really… But it’s surprising how little it comes up in everyday conversation.
I am not a musician. From a Fibonacci keyboard I noticed that 8/5 = 1.6 13/8 = 1.625. I am interested in the Golden Mean, 1.618… It is not a ratio. Does the Black Sabbath play irrational numbers? The Golden Mean is unique because the reciprocal of 1.618… = 0.618… Are reciprocals used in music?
An impulse (quantum) of light carries the frequency with it. Energy equals ( frequency multiplied by Planck’s constant). Studying the high frequencies of light lead to quantum mechanics. Your question is a good one. Einstein asked a related question and won the Nobel Prize for answering it. He conceptualized the quantum of light and named it the photon, similar to Adam naming a new animal. Think of light like an apple. An apple is red and crunchy both. Light is a wave and a particle both. What it appears to be depends upon how you are measuring it. Sometimes it appears to be a wave, and sometimes it appears to be a photon. The frequency of light will not change when photons come together coherently. They will become a laser beam, still the same color as the individual photons.
Pingback: WesMontgomeryBook.com · An amazing demonstration of rhythm becoming pitch and returning to rhythm again
Very nice! Please check out my site I have a video that explains rhythm… ALL of RHYTHM and more…. SALUDOS!
http://www.rhythmlineinstitute.com/#!join-the-conversation/c1whx
http://www.rhythmlineinstitute.com/#!books-1st/c12fs
http://www.rhythmlineinstitute.com/#!videos/c1vc4
http://www.rhythmlineinstitute.com/#!support/c1aoj
Rhythm is a NATURAL EVENT…. and even though westerners are not very aware of it other cultures have studied it… and ALL ETHNIC music is a manifestation of it(as well as everything in nature) as I show in my website and video. People in the western world try to INVENT a way to use these relationships without knowing how it manifests naturally and it sounds WEIRD!!!
NICE WEBSITE THOUGH…. thanks!!!
Pingback: Music | Pearltrees
you’ve stumbled on the secret of what makes harmony Dan.
In any chord there are interference patterns produced between the notes that make up the chord; when these “beat frequencies” enter the audible range they create phantom harmonics, some of which can even be below the level of the fundamental. An interval of a fifth for example, say A 440 to E 660 produces an interference pattern of beating at 220 Hz, well inside the audible range. Although we are not aware of this as a separate note sounding an octave below the root note of the chord, it’s what gives the interval it’s character. Invert it, and you have a phantom harmonic sounding two octaves below the A and an octave + a fifth below the root, giving the interval a subtly different character again. Interference patterns even occur between harmonics in the same resonant system.
Very good blog post.
Very interesting post. What was the most fascinating thing about it was the vibrating interval part. I’m a trumpet player and I noticed that each one of the notes you put on that staff (aside from the lowest one) are all possible to make without any valves being pressed down, and just by blowing faster air, and subsequently making more vibrations. So seeing that made me think a bit more of the mechanics of how a trumpet works..
Hey Andrew, glad this got you thinking a little more about the physics behind music. They’re definitely a big part of how the trumpet works! The Harmonic Experience, by W.A. Mathieu, is a fantastic book if you’d like to go deeper into both musical physics and how tonal harmony emerged from it.
I’m a trumpet player too, Andrew!
You’re totally right, those notes Dan wrote about as being on divisions of a string are exactly the same divisions of the tube in a trumpet. Increase lip frequency and you access the next higher note in the natural harmonic series. Press a combination of keys down and you change the length of the tube, which offers a whole new set of those natural harmonics, but on a different ‘fundamental’ bass note. Same thing works for any ‘tube’, like a vacuum cleaner hose or a half-drunk bottle of cider.
Strangely though, trumpets (and I guess other such horns) can’t access the lowest note (like strings can), the octave interval; we start from C and the next up is G. I think this must arise from the specific geometry of trumpet mouthpieces, tubing, etc. suppressing the resonance of the fundamental.
Well said, Sam.
I do similar experiments with an analogue synthesizer: use the envelope shaper, with increasingly fast envelope cycles, as a separate oscillator; or use ring modulation to generate a third tone (something to do at home with your washing machine on its spin cycle – hum exactly the same pitch then “detune” yourself very slightly and listen for the new third rhythm-become-tone: great party trick!)
Another thought: how would this “look” to people with synesthesia? Do particular rhythms have colour for them in the same way that certain pitches or keys (Just reading Oliver Sack’s ‘Musicophilia’, which inspires this comment)
Great question, Peter. Sacks presents cases of people with all kinds of synesthesia, so I wouldn’t be surprised if there were people out there who had sensory associations to particular rhythms. Love that book, btw.
anyone else hear some kind of ‘flash’ when crossing the threshold back from tone to rhythm? it’s just a moment when it ‘seems’ (hear-ms) like the gestalt shift crosses, where it takes/makes-a place where the rhythmic clicks of absence ‘stand up’, and are no longer sub-ordinated to (subsumed by) the tonal figure, but without yet having been turned ‘inside-out’ and again subordinated by the rhythmic (phrasal) figure.
I like that! I think I do hear something like that, yes.
What are the ratios for Aug, Dim, Maj b5, Sus2 (1 2 5) and Sus4 (1 4 5) triads? Thanks for the great work and post! 🙂
– Arco
Hi Arco,
You can figure this out by thinking about the frequency ratios of the harmonic series. A Sus 4 chord (C F Bb for example) is two stacked perfect fourths. From the harmonic series we know that a tone a perfect fourth above a fundamental vibrates at 4/3 the rate of the fundamental. So we can apply that twice to get 1 ; 4/3 ; 4/3*4/3, which you can simplify to 9 ; 12 ; 16.
(A caveat: in equal tempered tuning, all the intervals are slightly different from the natural ratios we find in the harmonic series, so the ratios above won’t give you exactly the same “perfect fourth” you’ll hear when you play the interval on a piano, but it’s close. Major thirds are quite noticeably different, however).
Dan
Anyone else hearing those ‘wind chime’ sounds in the intermediate phases (i.e. after rhythm discernment and before pitch detection)?
Are they computational artefacts?
Are they perceptual resonances arising from the increasing tempo?
Are they just the crazy impulse rhythms interacting with my tinnitus?
I thought I heard it before but, listening again, now I think my confirmation bias has kicked in.
Psychoacoustics is coooll.
Actually, it still can be heard after the pitch becomes clear.
Maybe somebody already commented on this, but I’m pretty sure Ezra Pound (!) talks in similar terms about this, but without the convenience of letting us hear the this stunning examples. He didn’t go as far as to harmony, as I recall.
CO
Wow, that’s certainly news to me. Would love to know where in Pound’s work this is.
Thanks. I was poring thru Hal Chamberlin’s “Musical Applications of Microprocessors” trying to understand how the speaker clicks on a reacquired Apple II could produce a pitch without the requisite DAC. Your explanation nailed it for me. Now for the fun of programming this in 6502 assembler.
And thanks for sharing your journey through the Goldbergs and the amazing mathematic tour-de-force displayed and hidden in the notes! Fascinating reading.
Many thanks, Stephen, glad this was interesting to you. I remember asking myself the same question about a TI-89 calculator in the 90s that someone had programmed to output rudimentary music…
I’ve been looking for this forever. Thank you so much! Its not very often i google something and find what im looking for. Food for thought, maybe timbre and composition is a fractal mess, imagine taking those rhythms, putting tones to them, and speeding them up. Also.. speed up the planets in our solar system a couple octaves, and whamo. the human hearing range. blows my mind how reality works. literally. I am typing this for muscle memory as my last dying wish haha
Pingback: Thinking of rhythem like pitch
Pingback: The Charm of Impossibilities: why music is magic – Infinite Genius
I found this post via Alexander Chen’s notes on the making of Chrome Music Lab, and let me extend you a hearty thanks for putting it together. I keep trying to explain this concept to students, and you’ve saved me a lot of trouble, because now I can just send them here.
Hi Dan,
Thank you so much for this blog post, I reference it in my orchestra class and Music Theory class at least annually. Your post is eye-opening and “mind-blowing” for those musicians, but is written with a lot of clarity. It often starts a very interesting discussion
There is one small thing I disagree with and I wanted to see what you thought. I don’t think the minor triad is (necessarily) a simpler rhythm at all. To me, it seems that way only because of the number of beats you chose to use to express each of them. If the major triad was expressed over 30 beats instead of 10, it wouldn’t have any triplets of course. Likewise, a minor triad can be expressed over only 10 beats, but using triplets. (But it’s not pretty – see the link below.)
http://i.imgur.com/4Rt8wdn.jpg
It doesn’t seem there is anything about a 4-5-6 pattern that necessarily uses triplets, or about a 10-12-15 that doesn’t use them. Neither uses them over 30 quarter notes, and they both use them over 10 quarter notes.
I hope this doesn’t seem pedantic – what are your thoughts?
Hi Jeff,


This is one of my favorite comments on this post so far. Great point. I have to agree with you from a theoretical perspective (of course you’re right on the math front) and disagree with you slightly on the practical front, because of the matter of density. Here’s the major triad (4/5/6) expressed over 30 beats, both in 30/4 and 3/4:
The major triad has a total of 15 events stretched over those 30 beats. The minor triad (10/12/15, here also over 30 beats)
packs 37 events into the same number of beats. As a player, if you’re going to compare the two rhythms, you’re going to want to be comparing them at a similar density. To me, that means presenting the 5/4 rhythm that happens in both between the E and G at the same density level, and seeing how the third voice behaves against that rhythm. At that scale, in the major triad we’re going to experience a ternary / binary rub that we’re not going to experience in the minor triad. Does that make sense to you? In other words, I do think, all other things being equal, that what I said applies when you’re playing the rhythms, even if it might not if you’re thinking about them.
Thanks again for the insightful comment.
Very nice work!
I wonder how a repetitive progression (say I, IV, V) would sound if decelerated to the point of turning into clicks.
Good question! That would depend on what voice leading you decide to use for the progression. If, for example, you were in C and started with C,E,G (ratios 4,5,6), then moved to C,F,A for the IV chord, with C staying as is (common tone), then you would move from ratios 4,5,6 to ratios 3,4,5. To represent the progression accurately you’d want the frequency of the C to stay the same, so you could have a metric modulation between the two chords so that the pulse of the 4 ratio stays the same when it moves to a 3 ratio. I’m excited to try that out…
Pingback: Using Harmonic Polyrhythms – Jack Ashley
Hey Dan – really great, lucid explanation of this. I wrote a follow-on from these ideas, would be interested to hear your thoughts! – http://jackashley.co.uk/2016/12/12/using-harmonic-polyrhythms/
Pitch and rhythm are both percepts related to periodicities of sound vibrations.
In the case of musical pitch, the periodicities of the repeating sound patterns are in the range of 25 to 4000 Hz (periods of 250 usec to 40 msec).
The phenomenon of the missing fundamental for pitch is explained in terms of temporal codes in the auditory system that are based on population-wide distributions of interspike intervals. Essentially, any repeating waveform with a fundamental in the range of ~25-4000 Hz and either a component at the fundamental or 3 harmonics below 4000 Hz will produce an F0 pitch at the fundamental.
Cariani, Peter A., and Bertrand Delgutte. 1996. Neural correlates of the pitch of complex tones. I. Pitch and pitch salience. J. Neurophysiol. 76 (3):1698-1716. II. Pitch shift, pitch ambiguity, phase-invariance, pitch circularity, and the dominance region for pitch. J. Neurophysiol. 76 (3):1717-1734.
Rhythmic patterns also have an analogous perceptual quality — any repeating pattern of events within periodicity limits will create an expectancy
of repetition at the fundamental period of the event-repetitions. This is experienced as a “chunk” or a “groove.” Rhythms are also temporally coded in the auditory system, at all levels, and similar kinds of time-domain representations and processing mechanisms are possible.
Cariani, Peter. 2002. Temporal codes, timing nets, and music perception. J. New Music Res. 30 (2):107-136.
A number of theorists in the past have noted the analogies between pitch and rhythm (pitch is a micro-rhythm).
SEE:
Boomsliter, P., and W. Creel. 1961. The long pattern hypothesis in harmony and hearing. J. Music Theory 5:2-31.
Pitch sequences (melodies) are invariant with respect to absolute frequency, being recognizable if frequency ratios are maintained, again, within limits (trasnpositional invariance). Analogously, rhythms are invariant with respect to tempo, being recognizable if ratios of time intervals between events are maintained, again within limits (tempo invariance of rhythm).
These invariances can be explained if the neural representations are in the time domain (they are temporal patterns of spikes) and if there are neural processing operations that can perform time-warping (such mechanisms are possible using tapped delay lines with different conduction velocities).
Hi Peter,
Thanks so much for this. I’ll dig into the papers you’re citing here and hope we can meet in person sometime.
Dan
Pingback: Fagottobooks Blog
Pingback: The Charm of Impossibilities ~ Why Music is Magic – LoveHasWon.org
Pingback: Bands by Fueled by Ramen – Phoebe's Btec Blog
Pingback: Bibliography – Phoebe's Btec Blog
Another question: what do you think it is happening here?
audio clip: https://we.tl/33mmZNcVG8
the pattern is –> | |||| |||| | | |||| |||||||||
But there is a fundamental pitch that won’t change. It’s fascinating. whyis this so?
Looking forward to your insights,
Gaha
Hi again, Gaha—
Unfortunately the transfer wasn’t available by the time I got to it.
Dan
Hi, thanks for replying. Here it is: https://goo.gl/dg5MsP
Another question that popped now is, how do you get the triad (major third) at all? I assume the previous examples worked because you had stetereo: one sound comes from L and another from R. For the triad trick to work the clicks must come from different spatial positions, otherwise they would combine and create one pitch… maybe. Could you explain this? Thanks in advance.
To answer your question, in the triad recordings the third note is in the middle (i.e. equally in L and R). But actually it doesn’t matter whether the clicks are spatialized at all. You can verify this by listening to the recordings in mono (on a single speaker, for example): your ear will hear all the different pitches regardless. Any periodic signal, even mixed together with others, will be detected by our ear as long as it’s within our range of hearing.
I see now. Did you have a chance to look at the clip? I wonder what is happening there. The pattern is –> | |||| |||| | | |||| |||||||||. But there is a fundamental pitch that won’t change, as I mentioned earlier. Thanks in advance.
Just checked it out. It seems that instead of using an unpitched “impulse”, you’re using a pitched sound for each one of the impulses. Your pitch is a B natural, so naturally it’s not going to change…
Thanks for the answer: “Your pitch is a B natural, so naturally it’s not going to change”. But you can hear the pitch increasing as a function of speed while other pitch stays the same. How do you explain this?
There are two pitches happening in your example: there’s the pitch of the impulse you’re using (a B natural), which doesn’t change, and there’s the perceived pitch made by the combined impulses as they get closer together, which does change depending on how close they are together. In my examples I am using an unpitched impulse, so the only pitch we hear is the pitch made by the combined impulses.
many many thanks!….fascinating!
Pingback: Rhythmic Thresholds: The Perceptual Present – Rhythmic Thresholds: The Perceptual Present
Pingback: Aliasing and the brain – Fundamentals of Linear Control: A Concise Approach
Pingback: Developing an intro-level music theory course | The Ethan Hein Blog
Hi Dan
Thank you for this great explanation on rhythm and pitch.
I don’t know if you know about Efrain Toro so I wanted to share this with you.
https://www.youtube.com/watch?v=jaYGbQZJlX8
This is such a great loop in the matrix! Efrain himself commented here in 2013!
Amazing post BTW, can you recommend more composers in this style of work?
Thanks!
Dear Dan,
thanks a lot for this post!
Reminded me on the work of Malcolm Braff, do you know him? He’s a pianist as you are and does a lot of research on rhythm and it’s relation to harmony.
With the same idea of rhythm and harmony being the same thing, he compares the special phrasing of rhythmical patterns in african or latin-american music with the tempering of our western twelve-tone-system. That’s why he describes Salsa as a major chord:
http://general-theory-of-rhythm.org/salsa-is-a-major-chord/
Wasn’t familiar with Braff but just checked him out, thanks! Looks like he’s very interested in this rhythm / pitch duality thing too, and from a different perspective. Very cool, thanks.
thank you! You’d mused in the original writing that perhaps flashes of light would make a color. The visual comparison to what you’re doing here is how our eyes/brain distinguish between still photos and “moving pictures” – seeing a series of individual images speed up and once it hits 24 frames per second, our brain interprets it as a flowing, moving image. It’s fascinating that the human ear is said to be able to hear frequencies from 20Hz – 20,000Hz. It’s right around the same cycles per second that our brain stops hearing or seeing separate, individual beats or images, and streams them together to form pitch & animation.
Also interesting is that you can record any sound, whether it’s a pulse, drum sound, clap, bird chirp, toilet flush, etc., and if you speed it up to 440Hz for example, it will sound like an A. No matter what sound we start with, if it is fast enough, it will create the same pitch at that frequency.
That’s an excellent analogy, thank you Angela, for the line between discrete and continuous perception of phenomena in the visual world. I hadn’t thought before about the fact that, as you point out, it occurs around the same frequency (20Hz, say) in both worlds.
Dan,
Wow, you’ve done a truly exemplary job explaining this topic! Thanks you.
Glad I could help, Ken.
This is amazing. Thank you. I hope I may ask a question.
I have searched the internet now for several days hoping to find an answer, to no avail.
Approximately at what frequency (BPM/Hz) do we cease to hear individual beats, and begin to hear a single continuous tone?
Say I tap a saucepan at 60 BPM, and each tap has a frequency of 440 Hz (perceived as a pitch of Middle A).
Assuming I was superhuman, how many times would I need to tap that saucepan per minute, (BPM) or per second (Hz) for it to be heard not as a percussive rhythm, but one long tone.
And, when that tone kicks in, will it be the frequency with which I am tapping, or will it be the frequency of the individual saucepan taps (440 Hz = Middle A)?
I know it takes time to answer questions and post these explanations, but I honestly have searched everywhere else for an answer to this.
Many thanks
Hi Paul, the answer to your first question is simple: you’re basically asking what the lowest frequency that humans can hear is. Below that, vibrations will be perceived as individual, separate events; above that, as a tone with a frequency. This lowest frequency is about 20 Hz (20 events per second). https://en.wikipedia.org/wiki/Hearing_range
Your second question is more complicated and depends on the nature of the individual taps. Do they have a clear attack and are they well separated from each other? Obviously if we allow them to blend into each other, we’ll just hear their own frequency (440Hz). But if they are separate, then we’ll hear the frequency at which we are tapping (as long as it’s above 20 Hz), or possibly some kind of combination of the two. If you read the other comments here, you’ll see that the composer Stockhausen explored exactly this idea in one of his pieces.
Hi, i do not hear the given rhythm, it is always only 4/4 that speeds up and becomes tone.
Hmmmm! Try listening again…
Pingback: Do Notes Show Pitch And Rhythm? – Almazrestaurant
The blogs you have produced are really convincing. It highlights the issues of key importance to the general public. Please keep it up .
Nice post https://urcomputertechnics.com/rhythmic-beat-of-the-1-across/
Very cool! I recently discovered this by myself while listening to extratone. Extratone is a genre of electronic music with a tempo above 3600 BPM, so the beats are heard as tones and intervals instead of rhythms and polyrhythms. Good job on your research! I may try making my own extratone songs later.