Ever since Five Pedals Deep, my trio record with Thomas Morgan and Ted Poor, came out in 2010, I’ve gotten a steady trickle of emails asking about a particular tune on it called Back Attya.
If you listen to it without knowing what it is, there’s something about the harmonic movement that might feel surprising. You can feel intuitively that it has a really solid structure, but at the same time, the chords don’t seem to move in a way that you would expect. There’s a reason for that: Back Attya, as the name cryptically suggests (ATTYA being an acronym), is an inversion of All The Things You Are, by Jerome Kern.
(An inversion, for our purposes here, is a chromatic inversion — a mirror image, with the mirror placed horizontally, where all the intervals are preserved exactly — not to be confused with a diatonic inversion. So if the original melody moves up by a major third, say, the inverted version moves down by a major third. A descending perfect fourth becomes an ascending perfect fourth, and so on. What note do you start on? More on that later.)
The first question I usually get about it is: “my friend told me that this was an inversion of All The Things You Are, and I can see how that works with the melody, but what’s going on with the harmony? Why is the first chord B Major?” At this point I tell people to look up saxophonist/theorist Steve Coleman’s theory of negative harmony, because my transformation of ATTYA above is basically a textbook application of that concept.
(I attended a couple of Steve’s workshops at the Jazz Gallery when I first moved to New York in 2006, and I learned a lot from them. Steve is exceptionally generous with sharing his ideas — where many people would keep them to themselves, he wants you to know his secrets.)
More often than not, I then get another email saying the person still couldn’t figure it out. Which I can understand, to a certain extent, because Steve rarely lays anything out in writing in an easily digestible way — he always goes deep, exploring every possible ramification of a topic. So I thought I’d explain my understanding of his method in as clear a way as possible, since 1) it’s a technique that can give gorgeous results and 2) it’s actually an application of very old musical ideas to jazz.
Here’s how you do it — from first principles:
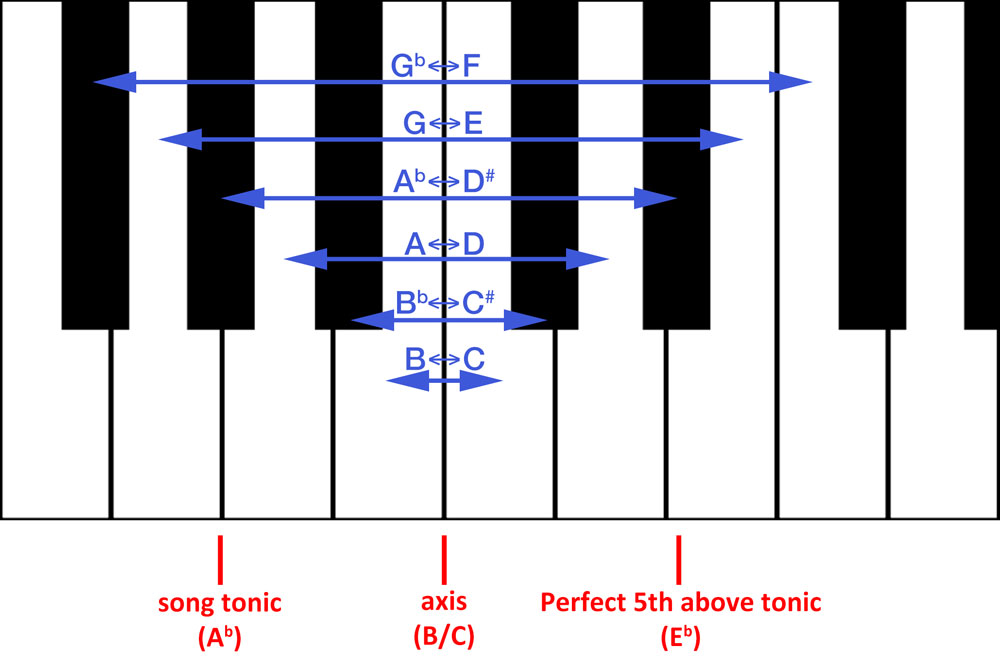
1. Find the key of the tune you want to invert. In the case of All The Things You Are, it’s Ab Major. The tonic of the song is Ab.
2. Determine the axis you’re going to use for the inversion. This will stay the same for the whole tune, even if the song temporarily modulates to another key. The axis is exactly half way between the tonic and the perfect fifth above it. In the case of ATTYA, half way between Ab and Eb puts the axis halfway between B and C:
3. Invert the melody around the axis. In the case of ATTYA, the axis is between B and C, so B inverts to C, Bb to Db, A to D, etc — and vice-versa (C becomes B, Db becomes Bb, etc).
The first melody note of ATTYA is Ab, which gives us Eb (or D#). Next one is Db, which gives us Bb (or A#), and so on.
4. Invert the harmony. This is a little more complicated but still pretty straightforward. The first chord of ATTYA is F minor — let’s ignore the 7th for now. F is the root of the chord. We invert this root around the axis to get F#, which we call the generator of the negative chord. Now, we recreate the original chord going down from this generator, rather than up. The notes of Fmin are F, Ab and C; moving up from the root, this is a minor third, then a major third. To get our inverted chord, we move down from the generator with the same sequence of intervals, first a minor third, then a major third. This gives us (reading downwards) F#, D# and B. We call this chord F# negative minor, or F#Nmin.
Now what shall we call this chord so that people who don’t know about negative harmony can read it? How do we name it in the positive world? This is really the key of Steve’s approach: the root of the negative chord is always a perfect fifth below the generator. This bears repeating: the root of the negative chord is always a perfect fifth below the generator. So the root (in the positive world) of F#Nmin is a perfect fifth below F#, which is B. Looking all the notes together (the root B, plus the notes we inverted — B, D# and F#), we see that we can simply call this B Major. This seems trivial in this case, but in other situations it’s not, as we’ll see.
Let’s look at the second chord of ATTYA, Bbmin7. Inverting around the B/C axis, as before, we get:
We’d be tempted to call this chord D#min7, but that would be wrong. Remember: the root in the positive world is always a perfect 5th below the generator. So the root of this chord is a perfect fifth below C#, i.e. F#. We call this chord F#6.
We’re almost there. Things get a little more complicated with chords that don’t already have a perfect fifth in them. The last chord of the bridge of ATTYA, C augmented, is a good example. Inverting around the B/C axis, the notes C, E, G# become B, G, D#. The root of this chord is a perfect fifth below B, so it’s E, even though that note isn’t present in the inverted notes. Looking at the combined notes, B, G, D# with an E root, we see that it’s an Emin(maj7) chord.
5. That’s it. Now play through the gorgeous results. As long as you’ve picked a tune with strong structure to start with, the negative version should have equally strong structure, but will often be unrecognizable. It’s amazing how much this straightforward, linear transformation completely changes the affect of a tune.
Here’s how you do it — the fast and easy way:
If you play around with what I explained above for a while — and you should definitely do it this way for a few tunes, if you really want to understand how this works — you’ll soon discover that producing negative harmony this way is the long way around. There are shortcuts you can take. Here’s the fast way:
1. Find the axis of symmetry, which is always exactly halfway between the tonic of the song and the perfect fifth above that.
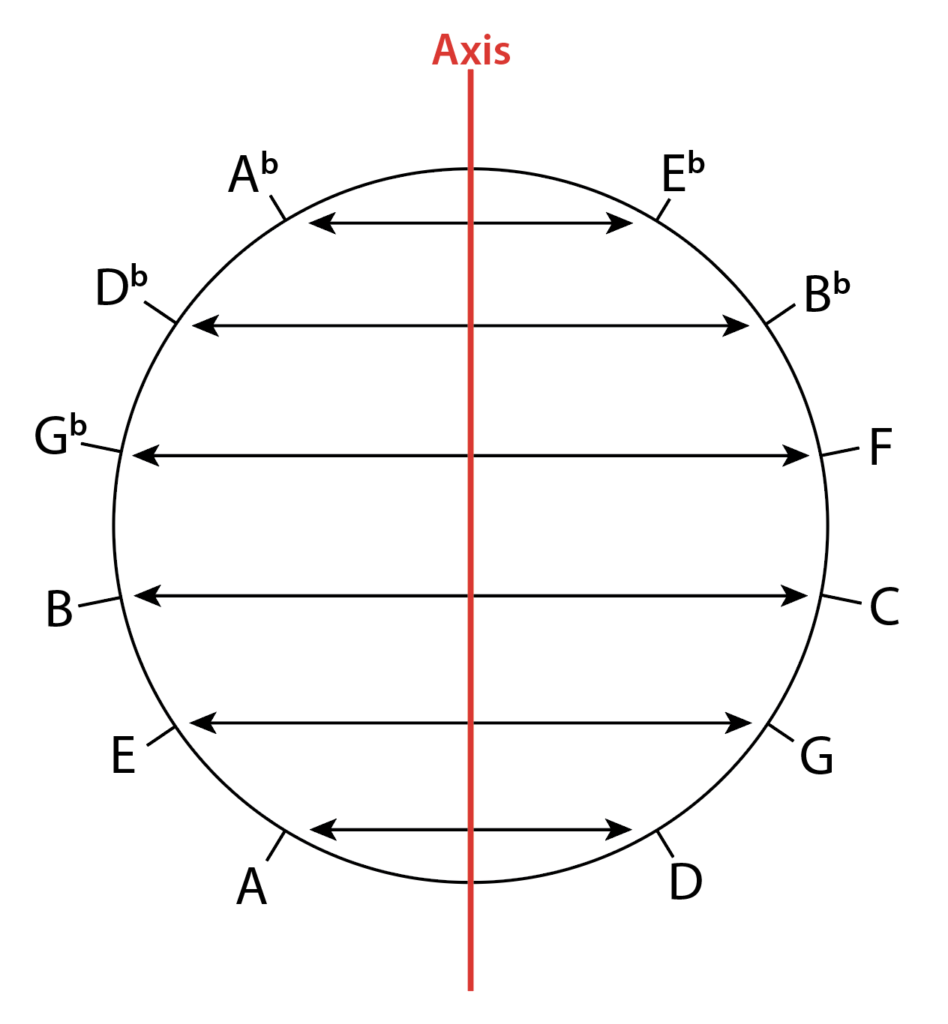
Here’s another way of looking at it using the circle of fifths, for the less piano-oriented. This is how my friend Ben Wendel likes to picture it:
2. Invert the melody around this axis, preserving all the intervals exactly (i.e. perform a chromatic inversion, not a diatonic one).

3. Find the chord roots for the inversion: invert the chord roots of the original song the same way as the melody, then transpose them all a perfect fifth down.

4. Notice that chord types always invert to the same chord type.
minor ⇄ Major
min7 ⇄ Maj6
Maj7 ⇄ min(b6)
7 ⇄ min6
5. Fill in the blanks

6. Enjoy!








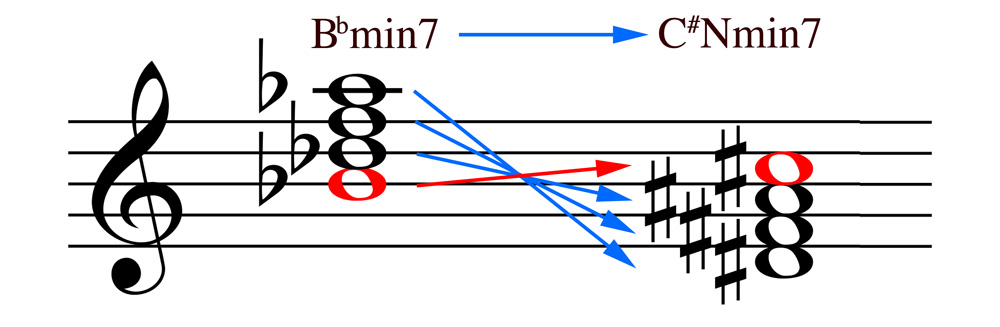


Hey Dan! Just wondering about your example of inverting Bbmin7? If flipped over the B/C axis, it should come out to be F#6? Not E6? As it is in your chord progression for Back Attya. Thanks!
Ooof! Wrote this way too late at night. Thanks much for catching this, just fixed it!
Hey Dan, thanks for blogging on negative harmony.
Just wondering about the diagram of the cycle of fifths,
It seems to be for negative generators in Db Major rather than Ab Major?
Cheers
Absolutely! Was for Db Major, not for Ab. Another late-night blogging incident. Just fixed it… Thanks Barney.
Thank you for this! It’s one of the simplest, crystal clear explanation I’ve seen!
Small question: when you show the circle of fifths that Ben Wendel uses, I assume this is for Db tonality, not for Ab tonality as in the ATTYA given example.
Yes indeed. Just moved it to Ab…
Ah, now I get that “fifth below the generator is the root” rule – it maintains the exact inversion of the root relationships to the tonic key, which is way more interesting than just inverting the chords and using the root it gives you, which would not be that interesting – , i.e. o7 chords would just invert right back into o7, etc. Honestly, I think this is much richer than the way Webern did this kind of stuff because it takes that robotic inversion operation and connects it to tonal harmony in a meaningful way.
Nice post, Dan!
Hey Nathan, that’s exactly it — by doing the perfect fifth down rule, you maintain the bass line movement (inverted), and you also maintain the key center (e.g. Ab Maj —> G# min). Steve uses it to generate harmonic substitutions within a tune — like he’ll sometimes do the bridge on rhythm changes in negative, for example. Works because the key center is preserved.
Thank you for writing this! So much easier to understand than Jacob Collier’s explanation (maybe he doesn’t quite understand negative harmony?). I was a little confused by what you meant when you write “in the positive world.” For example:
“So the root (in the positive world” of F#Nmin is a perfect fifth below F#, which is B.”
“Remember: the root in the positive world is always a perfect 5th below the generator.”
In each sentence, I was thinking it should have been “in the negative world.” Am I missing something?
Hi Dean, Steve Coleman wrote to me last night to point out the same thing. This was actually intentional on my part, but I could definitely be explaining it better. What I meant to convey is that F#Nmin is the notation for the chord in the negative world — a theoretical world where people know how to read negative chord notation. But in the positive world — the world where people only read positive chords, which is the world we live in — we need to find a notation for this F#Nmin chord that people can read. And that is B Maj. I’m going to find a better way of saying this.
Hi Dan- this is awesome, thank you. One quick possible typo related to the comment above…in the relevant illustration you have Bb min7 -> BNmin7, but it should be C#Nmin7? I think?
Yes indeed, thanks for catching that. A remnant of the previous typo. Just fixed it! Whew.
Hey mate. Thank you so much for this concise and simple explanation. Brings back great memories of getting into this stuff many years ago. I still have my copy of the UK magazine JAZZ FM from 1991 where SC talks about these ideas. Almost every other sentence in the article is marked by a pink fluoro highlighter.
Just had a listen to Back Attya as well – lovely, like everything you put your hands to.
So just wondering, have you done any improvising using a negative harmonic approach to the improvised melody? Eg: If you heard an improvised simple two note phrase (C# ascending to F#) over the first chord of Back Attya (BM) but actually played the negative melody (Bb descending to F) instead. I don’t have the skill on the saxophone to be able to hear a phrase over a chord and then invert and play it negatively in real time. In fact just thinking about it almost breaks my brain, but I was wondering was something you had programmed your Disklavier to do? To have it only sound the notes Bb to F when you play C# to F# ?
Is this really Steve Coleman‘s concept? Steve talks about this, but I very much doubt he would claim to have “invented” it. These ideas pre-date Steve Coleman, don’t they?
It seems like it would be worthwhile to cite other examples of this concept in both Steve’s music as well as historical occurrences in composers such as Bartok et al.
Hi Rudresh, nice to find you here!
Yeah totally — as I mention in the post, the “negative harmony” concept is an application of very old — centuries at least, and probably millennia (ancient Greeks) — ideas to jazz. Inversion is ancient. It’s omnipresent in Bach and it far predates him. And Steve is clear about that. However, learning about this approach from him in my mid-twenties is what got me started on this journey with the plagal side of things, so I wanted to do right by that. And there’s also just the fact that I got tired of people asking me to explain how negative harmony works, so that’s really what this post is about — a document that I can point people to so that I don’t have to keep explaining it.
Hope you’re well, Rudresh.
“Plagal side of things” 🙂
I see what you did there
Rudresh,
These are basically polarity ideas, but it can be used all kinds of ways. I use it a certain way, which is actually quite different than Levy or the European art music approach. I come more out of an extension of the Von Freeman tradition.
However, if you go deep down the rabbit hole, you can arrive at some interesting tonal progressions (not just so-called chordal “harmony”, but all things dealing with tones and rhythm).
I made a basic Facebook post about it here:
https://www.facebook.com/mbaseconcept/posts/10156586052644708
I learned it from Bird, Von, Monk, Bud, Rollins, Trane, etc., but as sound, as none of these cats talked about what they were doing. I began to check out the theory much later, as I state in the Facebook post. I did add a few wrinkles, but I can say that about almost anything that I’m into.
Hi Dan,
Amazing stuff! I just discovered your fascinating work and site from the NYT Article by Mr. Tommasini. I’d like to ask you how the Yamaha Disklavier does this – is playback “upside down” a feature it has or if not does it support code you wrote in some modern open-source language? By the way, you play the traditional Goldbergs beautifully. Thanks in advance.
Paul
Hi Paul,
Thank you! Re. the Disklavier: it functions as a MIDI instrument, meaning it can be controlled by a computer. So the inversion is being produced by code I wrote in the computer. I did write it in an open-source language, SuperCollider, which I’m fond of!
My best,
Dan
Dan, this is the best and most intelligible explanation of negative harmony that I have heard of. Thanks for the patience and simplicity.
My pleasure! Thank you.
Hi Dan, coming here via the NYT article from Friday, as long-time Bach fanatic and hobby pianist. What you’ve done is fascinating beautiful and I love it! Thanks also for sharing the inverted scores!
I was confused about the after reading this post (following link from http://www.dantepfer.com/bachupsidedown/) where you say “Since the Goldbergs are in G Major, I’m inverting about the axis between E and F.”
According to your explanation here, we would invert G major on the axis midway between G and D: B-flat and B i.e. between the major and minor thirds. Indeed, looking at your scores and comparing them to Bach, that rule works. But then I see that the rule about inverting on the E/F axis has the same result, and I’m still trying to wrap my head around this.
Anyway, this is the most fascinating treatment of Bach I’m aware of since Wendy Carlos.
Hi Bryce,
Thanks for this great comment! Indeed, one of the many things I don’t cover in this primer on negative harmony, in the interest of keeping it as simple as possible, is the tritone equivalence of the axis. As you discovered, it’s the same to invert between E and F as it is to invert between Bb and B, although things will of course end up in a different octave.
For the #BachUpsideDown project applied to the Goldbergs, I had the choice to invert on the E/F or Bb/B axes. I also wanted the music to remain as much as possible in the same register, so I wanted to have my axis be as close to the middle of the piano as possible. It turns out that the mid-point of an 88-key piano is exactly between the E and F above middle C! So this is better than inverting on either one of the Bb/B axes on either side.
My best to you, and so glad you’re digging the music.
Dan
Totally understand the process. The only question for me is why the root of the negative chord always a fifth below the “generator” rather than than giving the new root the same treatment as the other tones? Is this an arbitrary decision by Coleman or is there some logical psycho/acoustic reason that substantiates this practice? Could he not just as easily have chosen to transpose the top note down an octave (or two in the case of extended chords – 9ths, 11ths, and 13ths)?
Have you ever looked into Alan Forte’s work with pitch class set theory?
It’s not arbitrary at all. First of all, there’s a need to preserve the integrity of the bass line. And the only way that can happen is to have it be at a fixed distance from the generator; otherwise we would lose a fundamental part of the identity of the original. Secondly, regarding the choice of the perfect fifth, there’s no other choice that makes sense. It all starts from considering the tonic of the key. Let’s say we’re in C Maj. Our axis is Eb / E. The notes of the tonic chord, C E G, get inverted to G Eb C. It would be strange to call this anything other than C minor, don’t you think? Furthermore, when a piece in C Maj is inverted around Eb / E, it will *sound* like it’s in C minor. This, combined with the need to preserve the integrity of the bass line, leads directly to the rules above.
Oh, and yes! I have studied Forte’s 12-tone stuff. It’s interesting but definitely a completely different conversation from this one, which is first and foremost about tonality — which dodecaphonism is designed to avoid.
This is fascinating. Thank you so much for writing this blog post to explain it all so clearly! I am sorely lacking in music theory, and I still could follow what you wrote. I had a question right at the beginning that lingers, though: why is the axis where it is? Why do you invert around the midpoint between 1 and 5 (between minor and major third) — or equivalently, a tritone below that, as a previous commenter asked about above.
I kind of assume there’s nothing arbitrary about this, but I would like to know why that is what’s used… instead of say, using the tonic itself as the axis or something else.
Also, I just discovered your Bach upside down project (and variations / variations), and I am so excited to listen further. Phenomenal. Thanks again. Thanks again. Thanks again.
Thanks for your kind words, Jacob! To answer your question, the axis is chosen so that the key center stays the same. Say we’re in C Major. If we choose the axis between Eb and E, (halfway between C and G), then C inverts to G, E to Eb, and G to C. So our tonic chord, C Major, inverts to c minor. This way we maintain our key center, i.e. a piece in C inverts to a piece in C. Of course Major will always invert to minor, and minor to Major.
Ah okay! This makes sense, right. In a way it is arbitrary, but I see that in that way the most natural choice is to maintain the key (but switch major/minor).
I guess another natural choice if we’re in C major, would be the axis as D… so C becomes E, E becomes C, and G becomes A, and the tonic chord inverts to its relative minor, Amin. Right?
I wouldn’t call it arbitrary, since it has a clear rationale. Other choices are possible, of course, but this is the only one that makes consistent sense. For example, if we use your idea, that’s fine for major keys, but for a minor key, in order to move to the relative major, we’d have to use an axis a perfect fourth above the tonic (so c min -> Eb Maj). And then what do you do for pieces that have no clear major or minor quality, or that are constantly moving between the two, like some pieces of Brahms’? Choosing the axis halfway between the tonic and fifth is really the only solution that makes sense.
I see. Thanks for the post, and for walking though this. And thanks again for the music.
Wow! You even made this stuff make delightful sense to an aging rock ‘n’ roller! Thank you!
I’m late to the party of your music and ideas and am looking forward to catching up.
If I hadn’t come across Internal Melodies in December, I’d still be in the sad dark about you.
P.S. that album should be Grammy nominated in several categories, just sayin’.
Thank you Jeff!